[TOC]
formula1: \(n==x\)
formula2: \(n!=x\)
formula3: (m==y)
formula4: [m!=y]
formula5: (k==z)
formula6: [k!=z]
参考目录:
博客整理
在文献1的做法中,
惯性导航中的一些问题
四元数的运算总结
离散与连续之间的关系,比较让人迷惑。
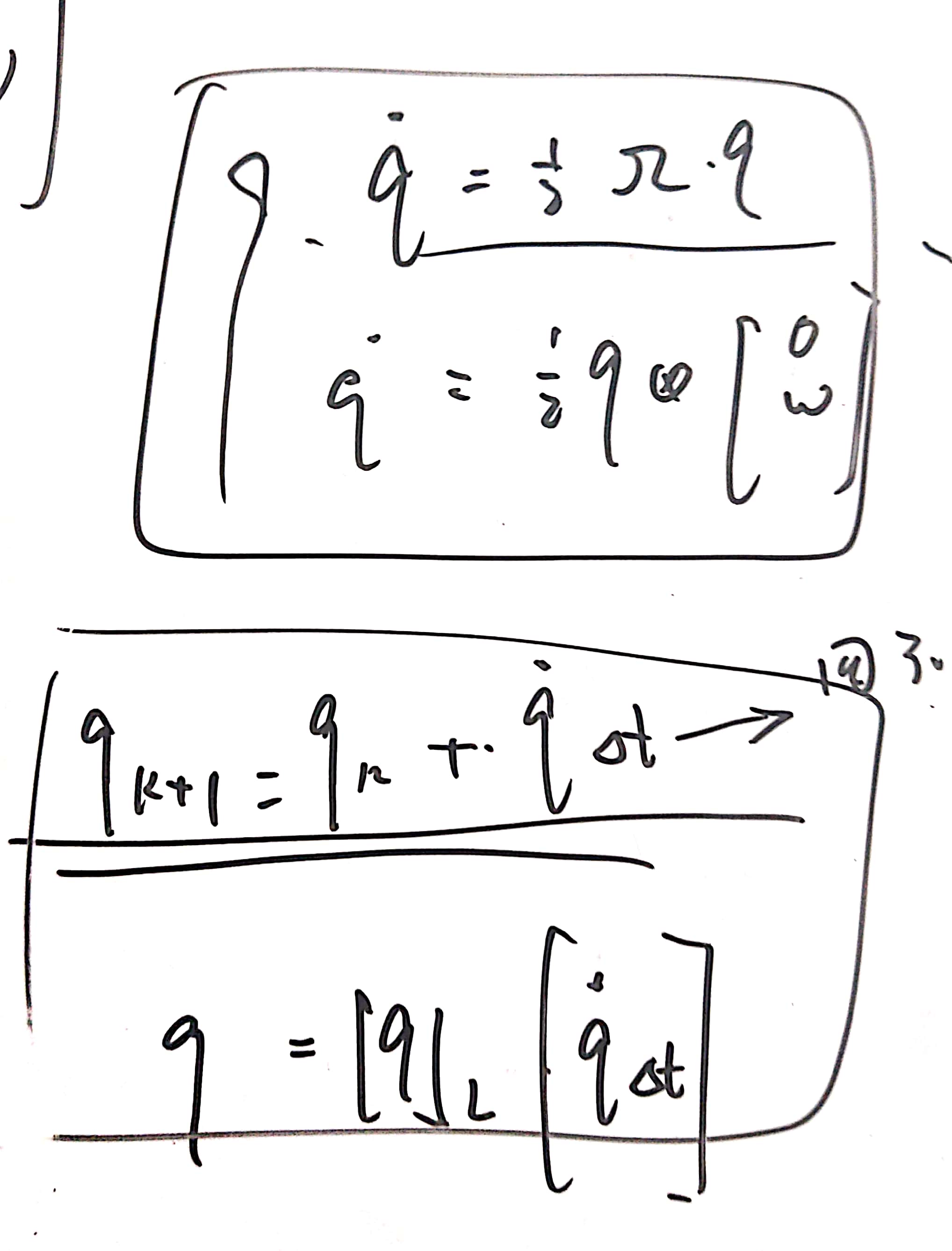
四元数的表示方法是什么?
可以这样表示: \(\dot{q}_{e}^{b}(t)=\frac{1}{2}\left[\begin{array}{cccc} 0 & -\omega_{x} & -\omega_{y} & -\omega_{z} \\ \omega_{x} & 0 & \omega_{z} & -\omega_{y} \\ \omega_{y} & -\omega_{z} & 0 & \omega_{x} \\ \omega_{z} & \omega_{y} & -\omega_{x} & 0 \end{array}\right] q_{e}^{b}(t)\) 在MEKF算法的差分化之后,有这样的结果: \(\boldsymbol{q}(t+\Delta t)=\boldsymbol{q}(t) \otimes e^{\frac{1}{2} \boldsymbol{q}_{\omega} \Delta t}\) 也可以表示为: \(\mathbf{q}_{b, b_{k}} \otimes \delta \mathbf{q}_{b_{k} b_{k}^{\prime}}=\delta \mathbf{q}_{b, b_{k}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \theta_{b_{k} b_{k}} \end{array}\right]\)
科式加速度的表示
参考;
科式加速度主要用来描述参考系与惯性系之间的关系。

我们来逐项分析上面这个式子。第一项中 αα 为 {B} 的角加速度,所以第一项的物理意义是 {B} 旋转所造成的 P 的切向加速度。第二项是 {B} 旋转所造成的向心加速度。第四项为 P 相对于 {B} 的加速度,但在惯性系 {A} 下表达——类似于 vrvr,定义相对加速度 arar。第三项比较特殊,为 {B} 的旋转运动与 P 相对 {B} 的平移运动耦合产生的加速度,称为「科氏加速度」。可以看到,除了第四项外,另外三项都和 {B} 的旋转有关。
什么时候能够用到科式加速度呢?
在MSCKF1中,考虑的是参考系(b),因此需要考虑;但在MSCKF2中,考虑的是惯性系(a),所以就不需要考虑科式加速度了。
这里存在一个问题:既然不考虑科式加速度又简便也符合逻辑,那么为什么一些文献中采用考虑科式加速度的做法呢?
在IMU中如何确定协方差矩阵?有没有一个简单的理解?或者通用的解释?
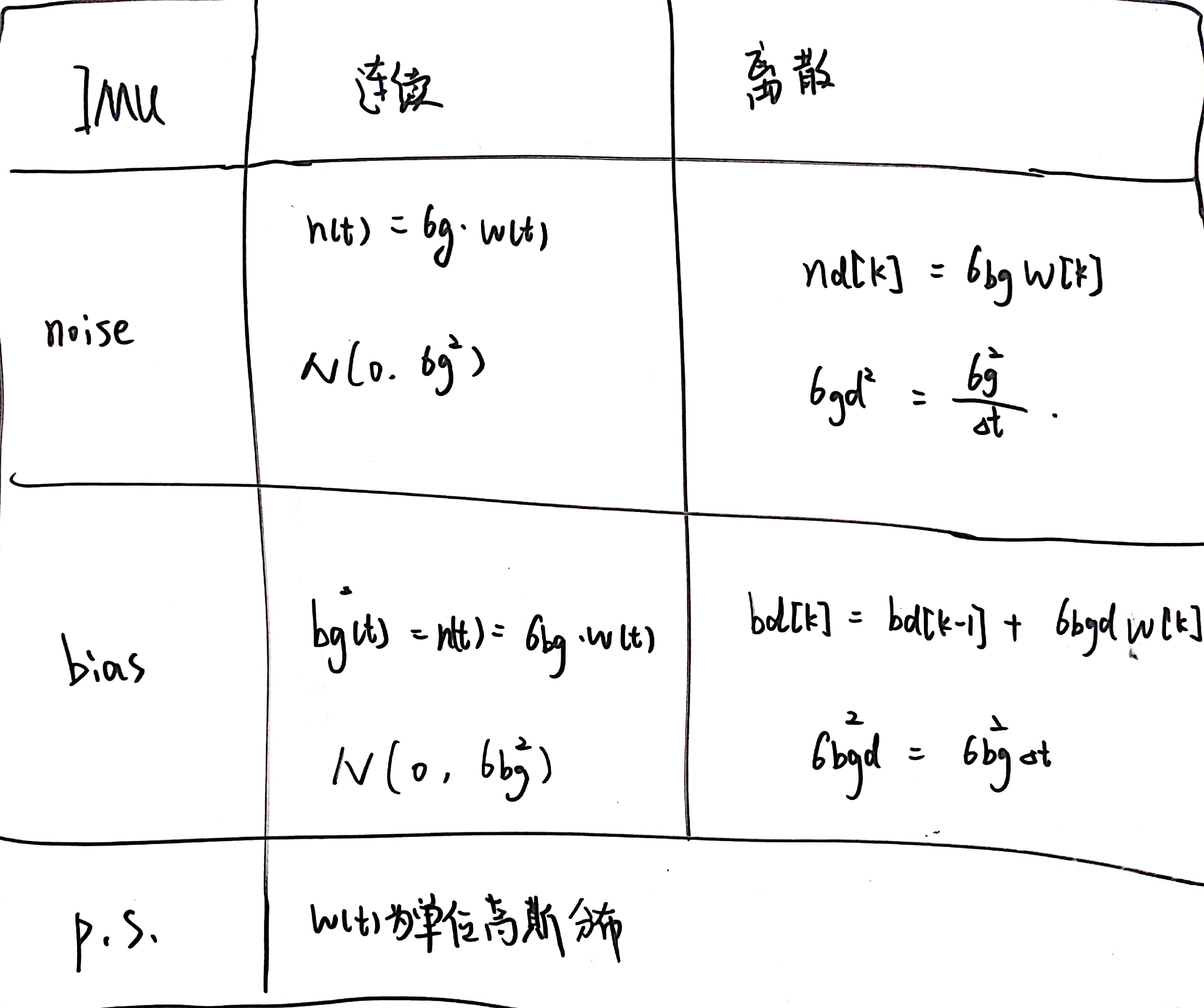
这里已经给出了比较合理的解释,可以根据这个关系去确定Q矩阵与R矩阵。上面的noise是白噪声,bias代表随机游走偏差,为白噪声的积分。
这里的问题是:这个部分到底是不是为了确定Q的大小?其实我觉得这里的描述未必准确。
这里给出了连续与离散之间的关系,但是实际上还有一层关系:积分与未积分的关系。
- 在之前的论文里是这么做的
我觉得这个和加速度计的固有性质相关。
- 博客的内容
计算方法如下:但是这里是白噪声还是随机游走?理论上应该是白噪声,因为没有讨论随机游走。 \(\frac{Q_{c}}{\Delta t} *{\Delta t}^{2}=\frac{b l k d i a g\left(\sigma_{g y r o}^{2}\right)}{\Delta t} *{\Delta t^{2}}\)
- 在博客中,提到一种ESKF的姿态角度估计方法,对于Q的求解,给出下面的结果:
但是这里面的加速度计于陀螺的表示都是一样的,怎么解释?
这里提到了一个积分的过程。
显然与上面的矛盾,这怎么处理呢?
如何确定协方差矩阵的更新?
要推导预积分量的协方差,我们需要知道 imu 噪声和预积分量 之间的线性递推关系。协方差矩阵可以这样推导:这个方差的积累公式需要注意一下,实际上状态估计大多都是这么做的。 \(\boldsymbol{\Sigma}_{i k}=\mathbf{F}_{k-1} \boldsymbol{\Sigma}_{i k-1} \mathbf{F}_{k-1}^{\top}+\mathbf{G}_{k-1} \boldsymbol{\Sigma}_{\mathbf{n}} \mathbf{G}_{k-1}^{\top}\) 其中,$Σ_n$ 是测量噪声的协方差矩阵,方差从 i 时刻开始进行递推,$Σ_{ii} = 0$。
但是在传统的卡尔曼滤波器的递推公式中,有下面的结果:

在这里更新的过程并没有考虑到控制量u的雅可比矩阵,这是为什么呢?因为u的雅可比矩阵只影响到P矩阵的更新,而并不影响标称值的更新。(标称值的更新依赖于更加准确的非线性状态更新方程)。
这里Q代表的过程误差方差矩阵,对应的维度是状态量。利用控制量与运动学方程,确实可以求出来状态量的误差方差矩阵。相当于状态量的方差有一部分是由控制量决定的。但是如果系统中没有控制量,只有状态量,那么就需要直接给出Q矩阵的值。实际上这种系统也是比较多的。
在一个开源项目中是这样确定Q的大小的:
sGPS = 0.5*8.8*dt**2 # assume 8.8m/s2 as maximum acceleration, forcing the vehicle
sCourse = 0.1*dt # assume 0.1rad/s as maximum turn rate for the vehicle
sVelocity= 8.8*dt # assume 8.8m/s2 as maximum acceleration, forcing the vehicle
sYaw = 1.0*dt # assume 1.0rad/s2 as the maximum turn rate acceleration for the vehicle
Q = np.diag([sGPS**2, sGPS**2, sCourse**2, sVelocity**2, sYaw**2])
可以看到这里的Q是用来描述连续微分运动学方程中的微分量的。因为这里的Q只是在定义误差量的过程噪声,所以是比较合理的。
最终在MEKF的博客中找到答案:
在文献1中找到下面的佐证(附录部分)。下面的差分化是利用了第二种状态方程的递推方法,然后进行离散化。

由此便得知协方差Q矩阵的确定过程。实际上在实验中,并没有特别严格的定义,实际上两种都可以。对比试验结果发现其影响比较小。
如何将角度积分差分化表示?
在VIO中,对于IMU的处理流程是:预积分–预积分的离散形式–推导预积分的方差。
| 类别 | 方法 |
|---|---|
| 博主 | 差分化–>离散化 |
| VIO | 离散化–>差分化 |
| 实际上就是两个部分:离散化,差分化。虽然都不是 什么复杂的数学理论,但是常常让人感到confused |

实际上IMU组件给系统系统的运动学方程,在状态估计中可以认为是一种约束。同时测量方程也可以认为是另外一种约束。
在优化系统中,将这两种约束都写入到优化函数中,并且保证惩罚函数是线性的,这样就可以利用梯度下降法简单求解了。
| 类别 | 方法 |
|---|---|
| 基于一阶泰勒展开误差递推方程:方法1 | 离散化–>差分化 |
| 基于误差随时间变化的递推方程:方法2 | 差分化–>离散化 |
| 备注 | 实际上就是两个部分:离散化,差分化。虽然都不是 什么复杂的数学理论,但是常常让人感到confused 另外,差分化就是将其写成误差状态的形式 |
但是因为方法2中需要知道状态量的连续导数关系(随时间变化的关系),很多系统都没办法求解这部分(在PVQ系统中可以做)。方法1中的离散形式比较符合对EKF的解释和EKF中协方差更新的方法,因此更加常用。
总结来说,如果系统是连续方程,那么需要先进行error state化之后再进行离散化。如果系统是离散方程,那么直接进行error state化即可。
下面是详细定义:

于是有下面的结果,这里的变化很重要:


但是最后一步是怎么推导的?
在上面的两种方法中,第一种是符合EKF的状态方程的递推关系的;第二种是目前VIO算法中的主流做法。应该是殊途同归的两种做法,但是第一种更为通用。
下面的推导是怎么完成的? \(\begin{array}{l} \dot{\delta \mathbf{v}}=\mathbf{R} \delta \mathbf{a}^{b}+\mathbf{R}[\delta \boldsymbol{\theta}]_{\times}\left(\mathbf{a}^{b}+\delta \mathbf{a}^{b}\right)+\delta \mathbf{g} \\ \dot{\delta \mathbf{v}}=\mathbf{R} \delta \mathbf{a}^{\mathbf{b}}-\mathbf{R}\left[\mathbf{a}^{b}\right]_{\times} \delta \boldsymbol{\theta}+\delta \mathbf{g} \end{array}\)
最符合逻辑的就是:两个小量相乘,最后的结果就是无穷小,可以忽略。
与ESKF的区别是什么?下面给出ESKF的定义。 \(\dot{\delta \mathbf{v}}=-\mathbf{R}\left[\mathbf{a}_{m}-\mathbf{a}_{b}\right]_{\times} \delta \boldsymbol{\theta}-\mathbf{R} \delta \mathbf{a}_{b}+\delta \mathbf{g}-\mathbf{R} \mathbf{a}_{n}\) 但是如何比较两者的区别?有待后续完成。
为什么要用误差状态量去表示呢?
这部分参考Quaternion kinematics for the error-state Kalman filte和博客。
- 定向误差状态是最小的,避免了与过度参数化相关的问题,以及相关协方差矩阵奇异性的风险,这通常是由强制约束引起的
- 误差状态系统总是在接近原始系统的情况下运行,因此远离可能的参数奇点、万向锁问题等,从而保证线性化的有效性始终保持不变
- 错误状态总是很小,这意味着所有二阶部分都可以忽略不计。这使得雅可比矩阵的计算变得非常简单和快速。有些雅可比数甚至可能是常数或等于可用状态量。
- 误差动力学是缓慢的,因为所有的大信号动力学都已集成到标称状态。这意味着我们可以以低于预测的速度应用KF修正
什么是动力学是缓慢的?变化是缓慢的?
是不是用来描述振动变化,有着更为出色的性能?如果是的话,这也是一个可以发论文的点。
是不是和李代数去表示是有关系的,只有在小量的时候,在切空间的性质才可以成立。
是如何将误差状态与控制量相结合的?
角速度积分表示: \(\begin{aligned} _{I}^{G} \dot{\boldsymbol{R}} &=_{I}^{G} \boldsymbol{R}\left[\boldsymbol{\omega}_{m}-\boldsymbol{b}_{g}-\boldsymbol{n}_{w}\right] \times \\ \dot{\boldsymbol{b}}_{g} &=\mathbf{0}+\boldsymbol{n}_{g} \end{aligned}\) 下面是旋转矩阵的积分过程: \(\frac{\mathrm{d} \mathbf{R}}{\mathrm{d} t}=\mathbf{R}[\boldsymbol{\omega}]_{\times}\) 得到离散化之后的: \(\mathbf{R}(t+\Delta t)=\mathbf{R}(t) e^{[\omega]_{\times} \Delta t}\)
参考EKF-Based IMU Orientation Estimation,有下面的运动学方程: \(\begin{aligned} \delta \boldsymbol{\theta} &=\operatorname{Exp}\left[\left(\boldsymbol{\omega}_{m}-\boldsymbol{b}_{g}\right) \Delta t\right]^{T} \delta \boldsymbol{\theta}-\delta \boldsymbol{b}_{g} \Delta t+\boldsymbol{\theta}_{i} \\ \delta \boldsymbol{b}_{g} &=\delta \boldsymbol{b}_{g}+\boldsymbol{\omega}_{i} \end{aligned}\) 表示为: \(\left[\begin{array}{c} \delta \boldsymbol{\theta} \\ \delta \boldsymbol{b}_{g} \end{array}\right]=\underbrace{\left[\begin{array}{cc} \operatorname{Exp}\left[\left(\boldsymbol{\omega}_{m}-\boldsymbol{b}_{g}\right) \Delta t\right]^{T} & -\boldsymbol{I} \Delta t \\ \boldsymbol{0} & \boldsymbol{I} \end{array}\right]}_{\boldsymbol{F}_{\boldsymbol{x}}}\left[\begin{array}{c} \boldsymbol{\delta} \boldsymbol{\theta} \\ \delta \boldsymbol{b}_{g} \end{array}\right]+\underbrace{\left[\begin{array}{cc} \boldsymbol{I} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{I} \end{array}\right]}_{\boldsymbol{F}_{i}}\left[\begin{array}{c} \boldsymbol{\theta}_{i} \\ \boldsymbol{\omega}_{i} \end{array}\right]\)
这里其实就说明了:sita与delta_sita的方差的对应关系。
四元数的运算是什么样的?
四元数相乘可以写成: \(\mathbf{q}_{1} \otimes \mathbf{q}_{2}=[\mathbf{q}]_{L} \mathbf{q}_{2}=[\mathbf{q}]_{R} \mathbf{q}\) 其中 \([\mathbf{q}]_{L}=\left[\begin{array}{cccc} q_{w} & -q_{x} & -q_{y} & -q_{z} \\ q_{x} & q_{w} & -q_{z} & q_{y} \\ q_{y} & q_{z} & q_{w} & -q_{x} \\ q_{z} & -q_{y} & q_{x} & q_{w} \end{array}\right]=q_{w} \mathbf{I}+\left[\begin{array}{cc} 0 & -\mathbf{q}_{v}^{\mathrm{T}} \\ \mathbf{q}_{v} & {\left[\mathbf{q}_{v}\right]_{\times}} \end{array}\right]\)
最后一点:四元数与李代数之间的关系?
- 首先是李代数的部分:
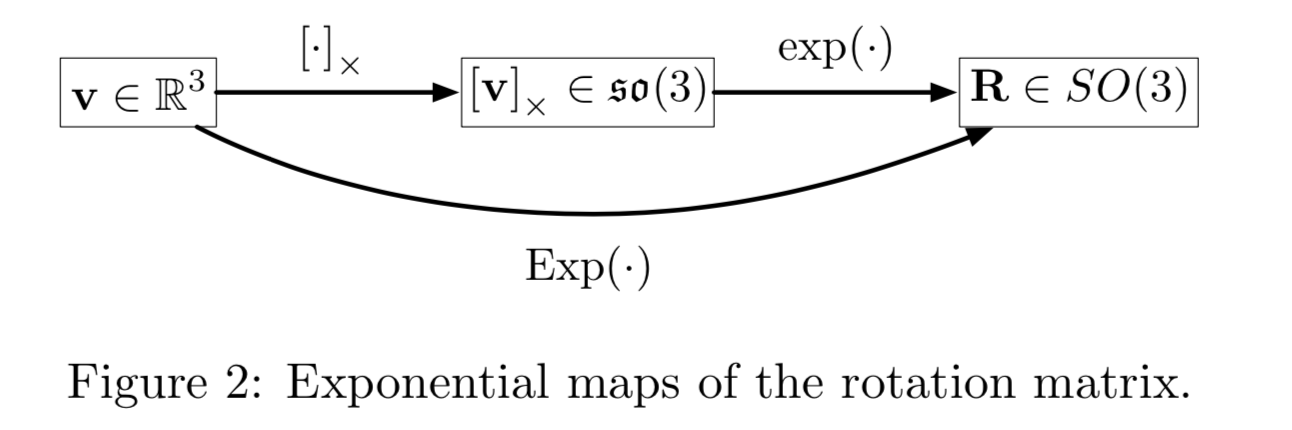
- 其次是罗德里格斯旋转公式:
- 描述旋转群与四元数之间的关系:参考文献1的 4.2.2
ESKF总结陈述
ESKF就是用了上述“基于误差随时间变化”求解方法,首先写成error state,然后进行离散化得到IMU的递推方程。/
参数表如下:

| English | 中文 |
|---|---|
| nominal state | 标称状态 |
| true state | 真实状态 |
| error state | 误差状态 |
首先是运动学方程中:
给出下面:

其中 𝜃𝑖 𝑤𝑖 为高斯随机脉冲噪声,均值为0,协方差为 𝑤𝑛 ,𝑤𝑏𝑛 在 𝛥𝑡时间内的积分值。
因此给出误差传播方程: \(\begin{aligned} \delta \mathbf{p} & \leftarrow \delta \mathbf{p}+\delta \mathbf{v} \Delta t \\ \delta \mathbf{v} & \leftarrow \delta \mathbf{v}+\left(-\mathbf{R}\left[\mathbf{a}_{m}-\mathbf{a}_{b}\right]_{\times} \delta \boldsymbol{\theta}-\mathbf{R} \delta \mathbf{a}_{b}+\delta \mathbf{g}\right) \Delta t+\mathbf{v}_{\mathbf{i}} \\ \delta \boldsymbol{\theta} & \leftarrow \mathbf{R}^{\top}\left\{\left(\boldsymbol{\omega}_{m}-\boldsymbol{\omega}_{b}\right) \Delta t\right\} \delta \boldsymbol{\theta}-\delta \boldsymbol{\omega}_{b} \Delta t+\boldsymbol{\theta}_{\mathbf{i}} \\ \delta \mathbf{a}_{b} & \leftarrow \delta \mathbf{a}_{b}+\mathbf{a}_{\mathbf{i}} \\ \delta \boldsymbol{\omega}_{b} & \leftarrow \delta \boldsymbol{\omega}_{b}+\boldsymbol{\omega}_{\mathbf{i}} \\ \delta \mathbf{g} & \leftarrow \delta \mathbf{g} \end{aligned}\)
其次是测量方程:
测量方程求取雅可比矩阵采用链式法则。
此外有:
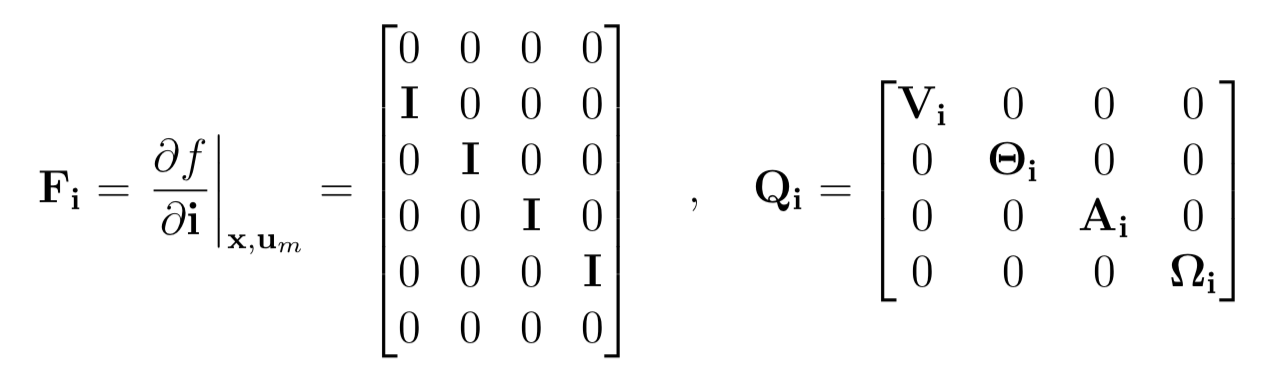 \(\left.\mathbf{X}_{\delta \mathbf{x}} \triangleq \frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\left[\begin{array}{ccc}
\mathbf{I}_{6} & 0 & 0 \\
0 & \mathbf{Q}_{\delta \boldsymbol{\theta}} & 0 \\
0 & 0 & \mathbf{I}_{9}
\end{array}\right]\)
总结来说,求取差分的偏导数如下,需要注意的是,我用到的是左栏的结果,右栏中未作考虑。
\(\left.\mathbf{X}_{\delta \mathbf{x}} \triangleq \frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\left[\begin{array}{ccc}
\mathbf{I}_{6} & 0 & 0 \\
0 & \mathbf{Q}_{\delta \boldsymbol{\theta}} & 0 \\
0 & 0 & \mathbf{I}_{9}
\end{array}\right]\)
总结来说,求取差分的偏导数如下,需要注意的是,我用到的是左栏的结果,右栏中未作考虑。
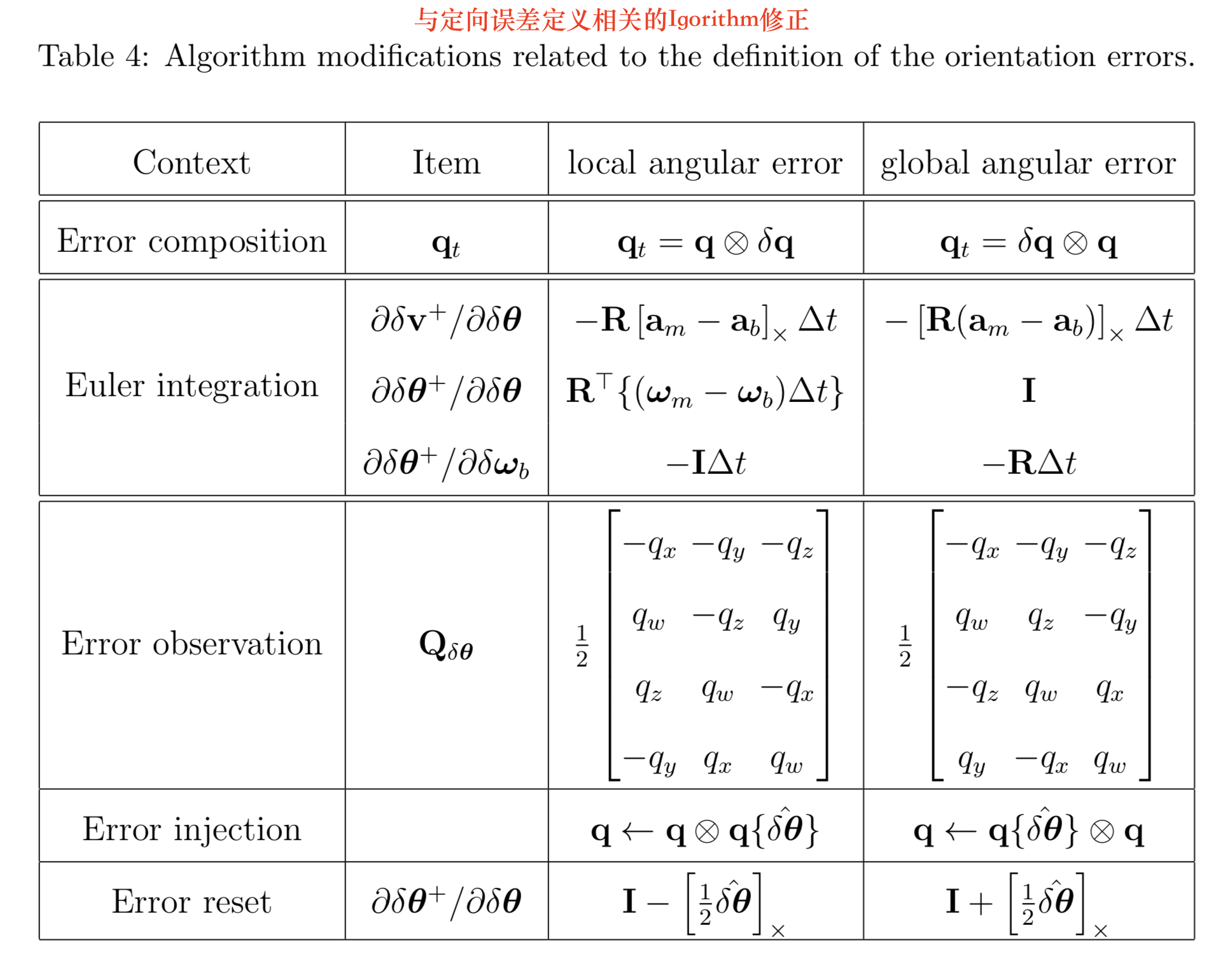
其中有比较重要的推导方法
下面是两种链式求导的方法,比较重要。 \(\left.\mathbf{H} \triangleq \frac{\partial h}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\left.\left.\frac{\partial h}{\partial \mathbf{x}_{t}}\right|_{\mathbf{x}} \frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\mathbf{H}_{\mathbf{x}} \mathbf{X}_{\delta \mathbf{x}}\)
\[\left.\mathbf{Q}_{\delta \boldsymbol{\theta}} \triangleq \frac{\partial(\mathbf{q} \otimes \delta \mathbf{q})}{\partial \delta \boldsymbol{\theta}}\right|_{\mathbf{q}}=\left.\left.\frac{\partial(\mathbf{q} \otimes \delta \mathbf{q})}{\partial \delta \mathbf{q}}\right|_{\mathbf{q}} \frac{\partial \delta \mathbf{q}}{\partial \delta \boldsymbol{\theta}}\right|_{\hat{\delta} \hat{\theta}=0}\]另外一个重要的性质,在其中的旋转矩阵表示为:
其中特别要注意四元数的旋转方式。
\(R=_{b}^{w}R=Exp[_{I}^{G}\delta\theta]=_{I}^{G}\delta q\)
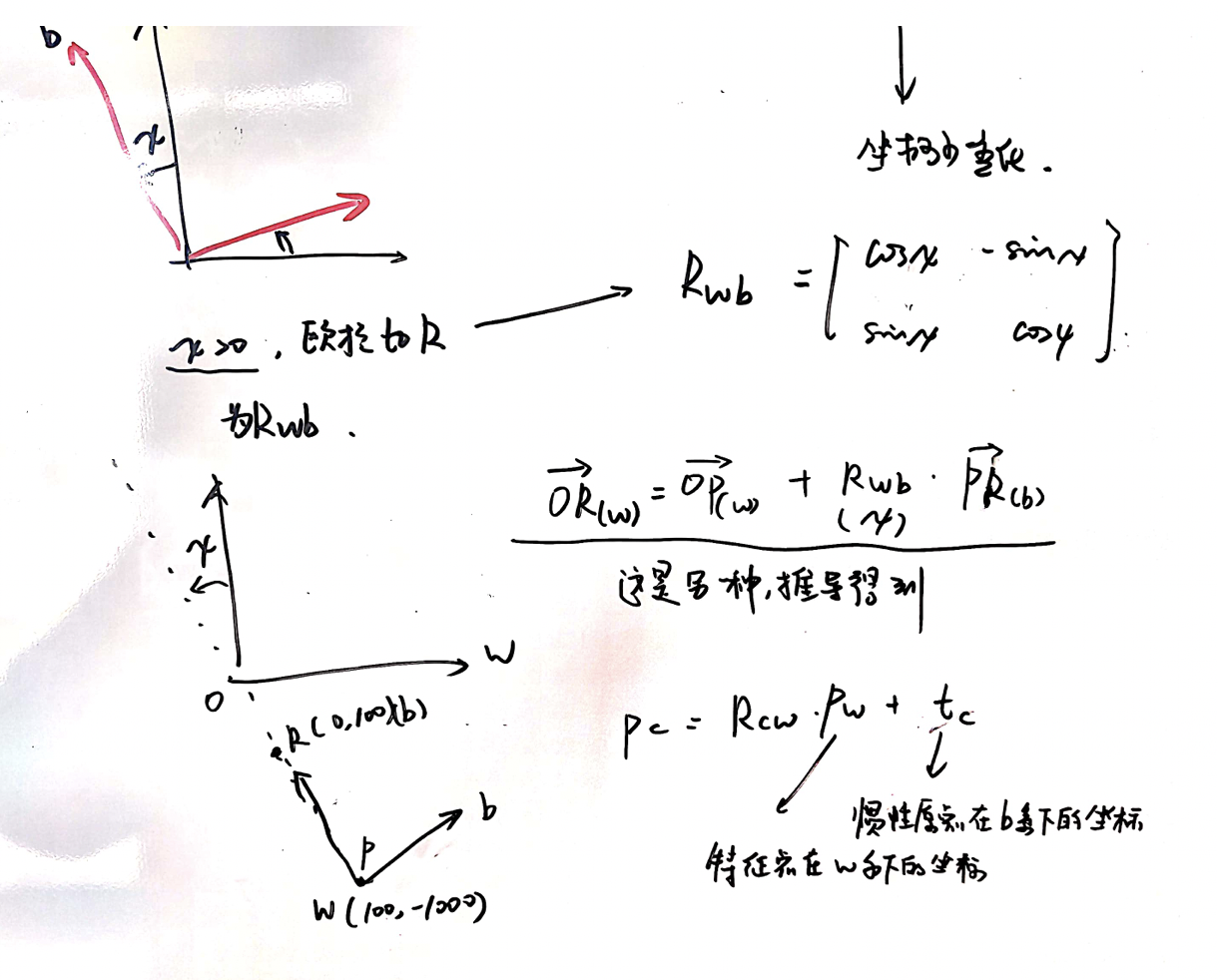
总体来说,需要区分标称值与误差状态量之间的关系。
cv中的3d标定:T21 = Tbw = 2d2d(pw,pb) = 2d2d(p1,p2)
欧拉角的表示
另外,观察到q与R都是有方向的,那么欧拉角有没有方向呢?事实证明是有的。

其中,W是可逆矩阵,这里说明了欧拉角也是存在方向的。上面说明了eulerRates与bodyRates之间的关系,下面表示了逆矩阵。
cr = cos(roll);
sr = sin(roll);
cp = cos(pitch);
sp = sin(pitch);
R = [1, 0, -sp;
0, cr, sr * cp;
0, -sr, cr * cp];
四元数中参与的运算
ESKF的实现
% =========================================================================
%
% ESKF的实现
%
%
% =========================================================================
%
% (C)2020-2022 China Academy of Railway Sciences
% 版本:V1.0
% 日期:2020年 6月23日
% 作者:s.m.
%--------------------------------------------------------------------------
% 功能:1.实现ESKF算法,加深对于状态估计的理解
% 2.其中的问题:
% 1) 测量加上地磁计
% 2) 注意误差量与标称量
% 3) 四元数转角度时有误差,就是这个导致了误差量
%
%
%
%--------------------------------------------------------------------------
clear all;
close all;
addpath('../../ESKF-Attitude-Estimation-master')
addpath('../utils')
% -------------------- import data-------------------
fileName = '../NAV_1';
Data = importdata(sprintf('%s.mat',fileName));
lengthtp = size(Data,1);
time = zeros(lengthtp,1);
roll = zeros(lengthtp,1);
pitch = zeros(lengthtp,1);
yaw = zeros(lengthtp,1);
imuNominalStates = cell(1,lengthtp);
imuErrorStates = cell(1,lengthtp);
measurements = cell(1,lengthtp);
%groundTruth
for state_k = 1:lengthtp
measurements{state_k}.dt = 0.02; % sampling times 50Hz
measurements{state_k}.omega = Data(state_k,27:29)';
measurements{state_k}.acc = Data(state_k,9:11)';
measurements{state_k}.mag = Data(state_k,15:17)';
time(state_k)=state_k*0.02;
end
rad2deg = 180/pi;
rollRef = Data(:,30)*rad2deg;
pitchRef = Data(:,31)*rad2deg;
yawRef = Data(:,32)*rad2deg;
% --------------------Data analysis------------------
% ++++++++++++++++++++1.initialization++++++++++++++++
dt = measurements{1}.dt;
% 怎么处理初始化的theta?
omega_b = zeros(3,1);%%这个用到
theta = zeros(3,1);%%这个用不到
% error state initialization
dt_theta = zeros(3,1);
dt_omega_b = zeros(3,1);
% Keep updated status
err_state = [dt_theta;dt_omega_b];
quat = zeros(4,1);
% --------Refer to previous practice for initialization-----------------------------------
init_angle = [Data(1,30),Data(1,31),Data(1,32)]';
init_quat = oula2q(init_angle);
quat = init_quat';
% -------------------------2.covariance matrix ---------------------
p1 = 1e-5;p2 = 1e-7;
P = blkdiag(p1,p1,p1,p2,p2,p2);%%初始化
sigma_wn = 1e-5;
sigma_wbn = 1e-9;
Theta_i = sigma_wn*dt^2*eye(3);
Omega_i = sigma_wbn*dt^2*eye(3);
Fi = eye(6);
Qi = blkdiag(Theta_i , Omega_i);
Q = Fi*Qi*Fi';
sigma_acc = 1e-3;
sigma_mn = 1e-4;
R = blkdiag(eye(3)*sigma_acc,eye(3)*sigma_mn);
for index = 1:lengthtp-1
% --------------------------forecast------------
omega_m = (measurements{index+1}.omega + measurements{index}.omega)/2;
av = (omega_m - omega_b)*dt;
det_q = [1;0.5*av];
quat = quatLeftComp(quat)*det_q;
omega_b = omega_b;
% 计算标称值
F1 = Exp_lee((measurements{index+1}.omega - omega_b)*dt);
F1 = F1';
Fx = [F1 , -eye(3)*dt;
zeros(3) , eye(3)];
P_ = Fx*P*Fx' + Q;
% -----------------------observation---------------------
% Prediction results and observations
[H,detZ] = calH(quat, measurements{index+1});
% --------------------update-----------------
K = P_*H'*inv(H*P_*H' + R)/2;
err_state = K*detZ;
P = P_ - K*(H*P_*H' + R)*K';
% ----------------------update state----------------------
% 参考之前的函数,dt_theta-->quat, quat的左乘方法
dt_theta = err_state(1:3);
dt_omega_b = err_state(4:6);
dt_q = buildUpdateQuat(dt_theta);
quat = quatLeftComp(quat)*dt_q;
quat = quat/norm(quat);
omega_b = omega_b + dt_omega_b;
% ------save angle-----------------------------
[a1,a2,a3] = quattoeuler(quat);
oula(index+1,:) = [a1,a2,a3]/180*pi;
dt_theta_save(index+1,:) = err_state';
% ----------------------------reset-------------------
err_state = zeros(6,1);
G = blkdiag(eye(3) - omegaMatrix(dt_theta/2) ,eye(3));
P = G*P*G';
end
% figure;
% subplot(3,1,1)
% plot(pitchRef);
% hold on;plot(oula(:,2)/pi*180);
% subplot(3,1,2)
% plot(rollRef);
% hold on;plot(oula(:,1)/pi*180);
% subplot(3,1,3)
% plot(yawRef);
% hold on;plot(oula(:,3)/pi*180);
% legend 1 2
rotLim = [-5 5];
figure;
subplot(3,1,1)
plot(oula(:,1)/pi*180 - rollRef);
subplot(3,1,2)
plot(oula(:,2)/pi*180 - pitchRef);
subplot(3,1,3)
plot(oula(:,3)/pi*180 - yawRef);
legend 1 2
% ylim(rotLim)
function R = q2R(q)
%四元数转旋转矩阵
R=[ 2*q(1).^2-1+2*q(2)^2 2*(q(2)*q(3)-q(1)*q(4)) 2*(q(2)*q(4)+q(1)*q(3));
2*(q(2)*q(3)+q(1)*q(4)) 2*q(1)^2-1+2*q(3)^2 2*(q(3)*q(4)-q(1)*q(2));
2*(q(2)*q(4)-q(1)*q(3)) 2*(q(3)*q(4)+q(1)*q(2)) 2*q(1)^2-1+2*q(4)^2];
R2 = R;
end
function Q_dt_theta = cal_Q_dt_theta(quat)
Q_dt_theta = 0.5* [-quat(2) -quat(3) -quat(4); ...
quat(1) -quat(4) quat(3); ...
quat(4) quat(1) -quat(2); ...
-quat(3) quat(2) quat(1)];
end
function F = Exp_lee(in)
S = omegaMatrix(in);
normV = sqrt(S(1,2)^2+S(1,3)^2+S(1,3)^2);
F = eye(3)+sin(normV)/normV*S(:,:)+...
(1-cos(normV))/normV^2*S(:,:)^2;
end
function [omega]=omegaMatrix(data)
% wx=data(1)*pi/180;
% wy=data(2)*pi/180;
% wz=data(3)*pi/180;
wx=data(1);
wy=data(2);
wz=data(3);
omega=[
0,-wz,wy;
wz,0,-wx;
-wy,wx,0
];
end
function q = R2q(R)
%旋转矩阵转四元数
t=sqrt(1+R(1,1)+R(2,2)+R(3,3))/2;
q=[t (R(3,2)-R(2,3))/(4*t) (R(1,3)-R(3,1))/(4*t) (R(2,1)-R(1,2))/(4*t)];
Q1 = q;
end
function q = oula2q(in)
x = in(1);
y = in(2);
z = in(3);
%欧拉角转四元数
q = [cos(x/2)*cos(y/2)*cos(z/2) + sin(x/2)*sin(y/2)*sin(z/2) ...
sin(x/2)*cos(y/2)*cos(z/2) - cos(x/2)*sin(y/2)*sin(z/2) ...
cos(x/2)*sin(y/2)*cos(z/2) + sin(x/2)*cos(y/2)*sin(z/2) ...
cos(x/2)*cos(y/2)*sin(z/2) - sin(x/2)*sin(y/2)*cos(z/2)];
end
function Ang3 = q2oula(q)
%四元数转欧拉角
x = atan2(2*(q(1)*q(2)+q(3)*q(4)),1 - 2*(q(2)^2+q(3)^2));
y = asin(2*(q(1)*q(3) - q(2)*q(4)));
z = atan2(2*(q(1)*q(4)+q(2)*q(3)),1 - 2*(q(3)^2+q(4)^2));
Ang3 = [x y z];
end
function updateQuat = buildUpdateQuat(deltaTheta)
deltaq = 0.5 * deltaTheta;
updateQuat = [1; deltaq];
updateQuat = updateQuat / norm(updateQuat);
end
function qLC = quatLeftComp(quat)
vector = quat(2:4);
scalar = quat(1);
qLC = [ scalar , -vector';
vector , scalar*eye(3) + crossMat(vector) ];
end
function [H,detZ] = calH(q,measurements_k)
% Normalise magnetometer measurement
if(norm(measurements_k.mag) == 0), return; end %
measurements_k.mag = measurements_k.mag / norm(measurements_k.mag); % normalise magnitude,very important!!!!
% Normalise accelerometer measurement
if(norm(measurements_k.acc) == 0), return; end % handle NaN
measurements_k.acc = measurements_k.acc / norm(measurements_k.acc); % normalise accelerometer ,very important!!!!
% Reference direction of Earth's magnetic feild
h = quaternProd(q, quaternProd([0; measurements_k.mag], quatInv(q)));
b = [0 norm([h(2) h(3)]) 0 h(4)];
Ha = [2*q(3), -2*q(4), 2*q(1), -2*q(2)
-2*q(2), -2*q(1), -2*q(4), -2*q(3)
0, 4*q(2), 4*q(3), 0];
Hm = [-2*b(4)*q(3), 2*b(4)*q(4), -4*b(2)*q(3)-2*b(4)*q(1), -4*b(2)*q(4)+2*b(4)*q(2)
-2*b(2)*q(4)+2*b(4)*q(2), 2*b(2)*q(3)+2*b(4)*q(1), 2*b(2)*q(2)+2*b(4)*q(4), -2*b(2)*q(1)+2*b(4)*q(3)
2*b(2)*q(3), 2*b(2)*q(4)-4*b(4)*q(2), 2*b(2)*q(1)-4*b(4)*q(3), 2*b(2)*q(2)];
Hx = [Ha, zeros(3,3)
Hm, zeros(3,3)];
% Hx = [Ha, zeros(3,3)];
Q_detTheta = [-q(2), -q(3), -q(4)
q(1), -q(4), q(3)
q(4), q(1), -q(2)
-q(3), q(2), q(1)];
Xx = [0.5*Q_detTheta , zeros(4,3)
zeros(3) , eye(3)];
H = Hx*Xx;
detZ_a = [ 2*(q(2)*q(4) - q(1)*q(3)) + measurements_k.acc(1)
2*(q(1)*q(2) + q(3)*q(4)) + measurements_k.acc(2)
2*(0.5 - q(2)^2 - q(3)^2) + measurements_k.acc(3)];
% detZ = detZ_a;
detZ_m =[((2*b(2)*(0.5 - q(3)^2 - q(4)^2) + 2*b(4)*(q(2)*q(4) - q(1)*q(3))) + measurements_k.mag(1))
((2*b(2)*(q(2)*q(3) - q(1)*q(4)) + 2*b(4)*(q(1)*q(2) + q(3)*q(4))) + measurements_k.mag(2))
((2*b(2)*(q(1)*q(3) + q(2)*q(4)) + 2*b(4)*(0.5 - q(2)^2 - q(3)^2)) + measurements_k.mag(3))];
detZ = [detZ_a;detZ_m];
end
function [roll,pitch,yaw] = quattoeuler(q)
rad2deg=180/pi;
T=[ 1 - 2 * (q(4) *q(4) + q(3) * q(3)) 2 * (q(2) * q(3) +q(1) * q(4)) 2 * (q(2) * q(4)-q(1) * q(3));
2 * (q(2) * q(3)-q(1) * q(4)) 1 - 2 * (q(4) *q(4) + q(2) * q(2)) 2 * (q(3) * q(4)+q(1) * q(2));
2 * (q(2) * q(4) +q(1) * q(3)) 2 * (q(3) * q(4)-q(1) * q(2)) 1 - 2 * (q(2) *q(2) + q(3) * q(3))];%cnb
roll = atan2(T(2,3),T(3,3))*rad2deg;
pitch = asin(-T(1,3))*rad2deg;
yaw = atan2(T(1,2),T(1,1))*rad2deg-8.3;%%这个固定偏差是什么鬼
yaw = atan2(T(1,2),T(1,1))*rad2deg;%%这个固定偏差是什么鬼
end
这里面一个很重要的性质就是: \(\delta q=\left[\begin{array}{l}1 \\ \frac{1}{2} \delta \theta\end{array}\right]\)





