[TOC]
0. 参考资料
1. 李群与李代数
李代数与李群的关系参考「SLAM14讲」。
尽管刚体的姿态有很多种不同的表示方法,它们的积分方法也不相同,但这其中有一些共通的地方,在这里作一些简要但不严格的介绍。刚体旋转群 SO(3) 是一个李群,所谓李群是指同时具有光滑流形和群的结构的空间,同时群内的运算也是光滑的。李群的定义需要花很长篇幅解释清楚,也不重要,在这篇文章中我们需要知道的是 SO(3) 上的每一个旋转,都有一个切空间。这个切空间是一个线性空间,它的维数与 SO(3) 相同,即具有三个自由度。在李群的语言中,切空间也叫做李代数(Lie Algebra)。切空间的直观理解是:切空间内的每一个向量代表了一个速度,并且这个速度可以通过李群的性质积分成一个位移,而这个积分就是李群的指数映射(exponential map)。可以证明指数映射在局部是一一对应的,也就是每个速度都对应了唯一一个位移。
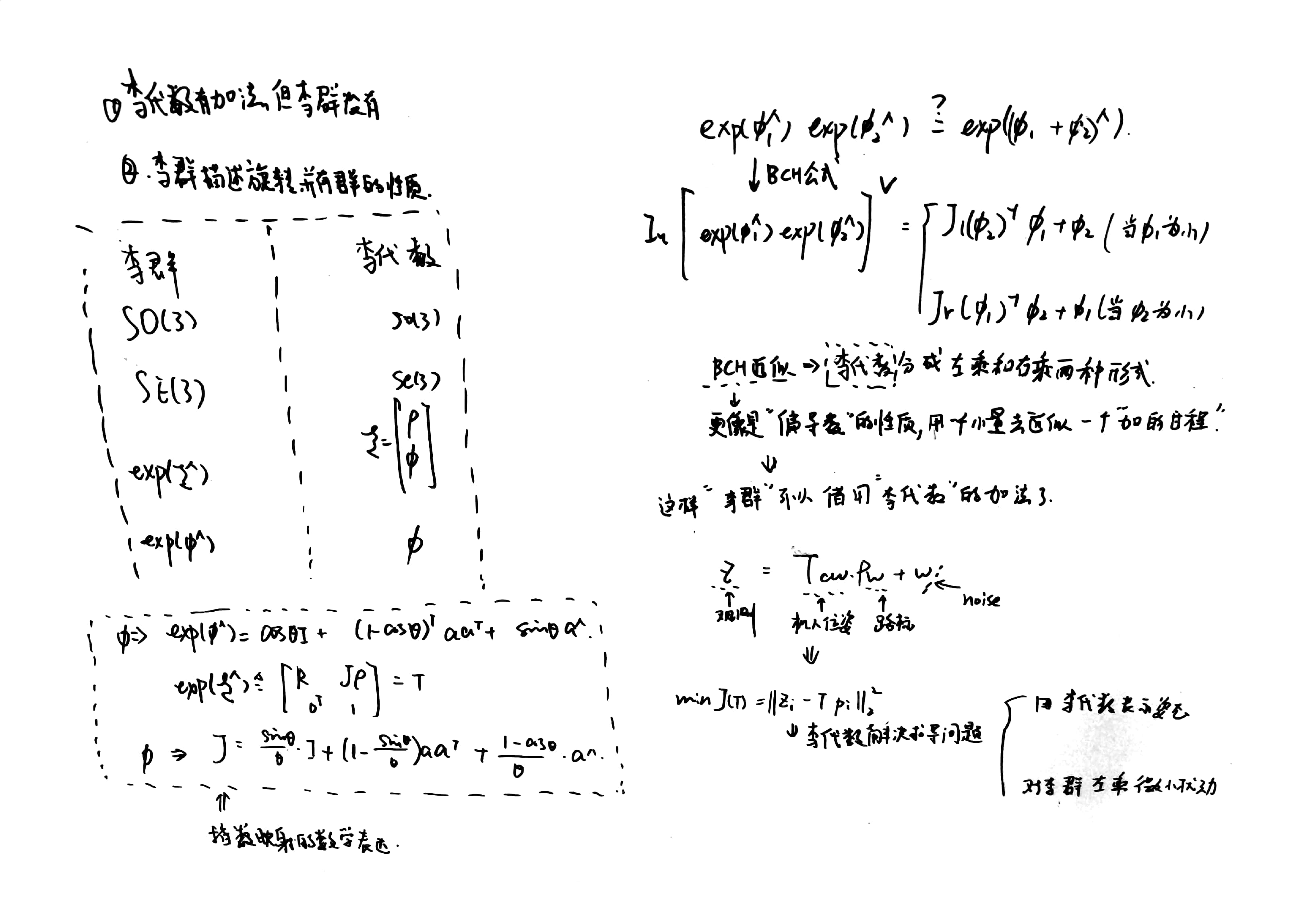
对上述理论引用到slam中去有下面的关系。
在三维表示中比较容易混淆的就是转换矩阵中的R与t的方向问题。下面记录一种比较直接的理解。 \(T_{w}^{c}=R_{w}^{c} P_{w}+t_{\overrightarrow{c w}}^{c}\) 下面对李代数相关问题进行求导。求微小的变化进行求导。
\[\lim _{\delta \xi \rightarrow 0} \frac{\exp \left([\delta \xi+\xi]_{\times}\right) P_{w}-\exp (\hat{\xi}) P_{w}}{\delta \xi} =\lim _{\delta \xi \rightarrow 0} \frac{\left[\mathbf{J}_{\ell}(\xi) \delta \xi\right]_{\times} P_{c}}{\delta \xi}=\left[\left[-P_{c}\right]_{\times}, \mathbf{I}_{3}\right]_{3 \times 6} \mathbf{J}_{\ell}\]假设雅可比矩阵为$\boldsymbol{H}=\frac{\partial h}{\partial \delta \boldsymbol{x}}$,可以用链式法则计算$\boldsymbol{H}=\frac{\partial h}{\partial \delta x}=\frac{\partial h}{\partial x} \frac{\partial x}{\partial \delta x}$。
那么如何对李代数的部分进行求导呢?
在SLAM中经常用到的李代数的内容,设定求解变换矩阵T的逆为: \(\boldsymbol{T}^{-1}=\left[\begin{array}{cc} \boldsymbol{R}^{T} & -\boldsymbol{R}^{T} \boldsymbol{t} \\ \boldsymbol{0}^{T} & 1 \end{array}\right]\)
假设有一个旋转轴为 n,角度为 θ 的旋转,由旋转向量到旋转矩阵的过程由罗德里格斯公式表明如下,同时,他们正是 SO(3) 上李群与李代 数的对应关系。 \(\boldsymbol{R}=\exp \left(\boldsymbol{\xi}^{\wedge}\right)=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{T}+\sin \theta \boldsymbol{n}^{\wedge}\) 对于SE(3)上的指数映射, \(\exp \left(\boldsymbol{\xi}^{\wedge}\right) \triangleq\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{J} \rho \\ \boldsymbol{0}^{T} & 1 \end{array}\right]=\boldsymbol{T}\) 雅可比矩阵可以写成: \(\boldsymbol{J}=\frac{\sin \theta}{\theta} \boldsymbol{I}+\left(1-\frac{\sin \theta}{\theta}\right) \boldsymbol{a} \boldsymbol{a}^{T}+\frac{1-\cos \theta}{\theta} \boldsymbol{a}^{\wedge}\) 下面的图直观的展示了这样的关系:

在对相机位姿的求导问题中,slam14讲 有比较直接的论述,主要有两个方向:
1. 直接对李代数求导,利用李代数的加法,但是存在难以消除的雅可比矩阵
2.左乘扰动的方法,并对扰动项进行求导,最后的结果更加简练
在slam十四讲中详细介绍了这两种求导的方法:
为什么对于微小变量的求导等于直接对变量进行求导?
假设$f(x)=x^2+2x$,直接对x求导:$2x+2$,然后对delta_x求导:$2\delta x+2x*2$。这一点很重要。
2. 图像处理基础知识
主要侧重于图像处理、特征点提取部分。
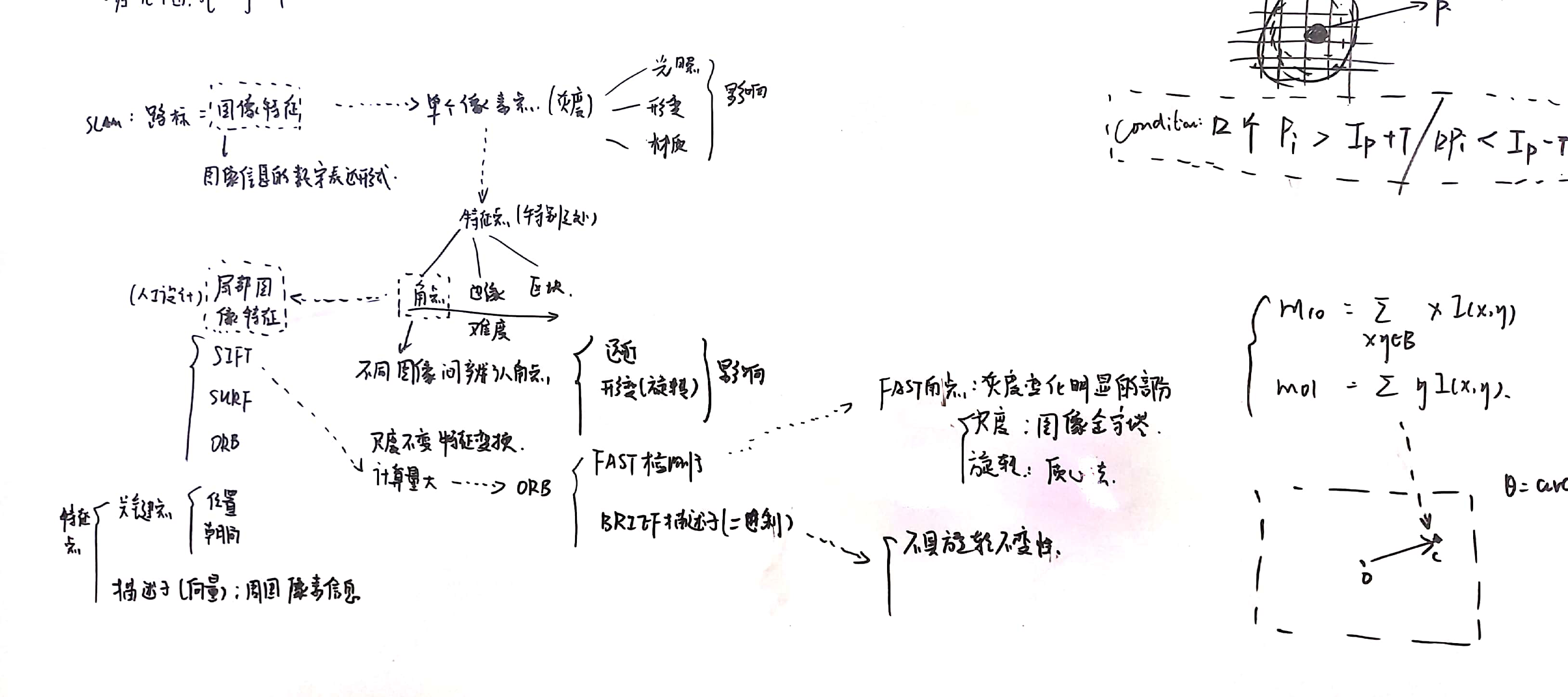
坐标系
3. 2D-2D 对极几何
这里的双目模型很重要
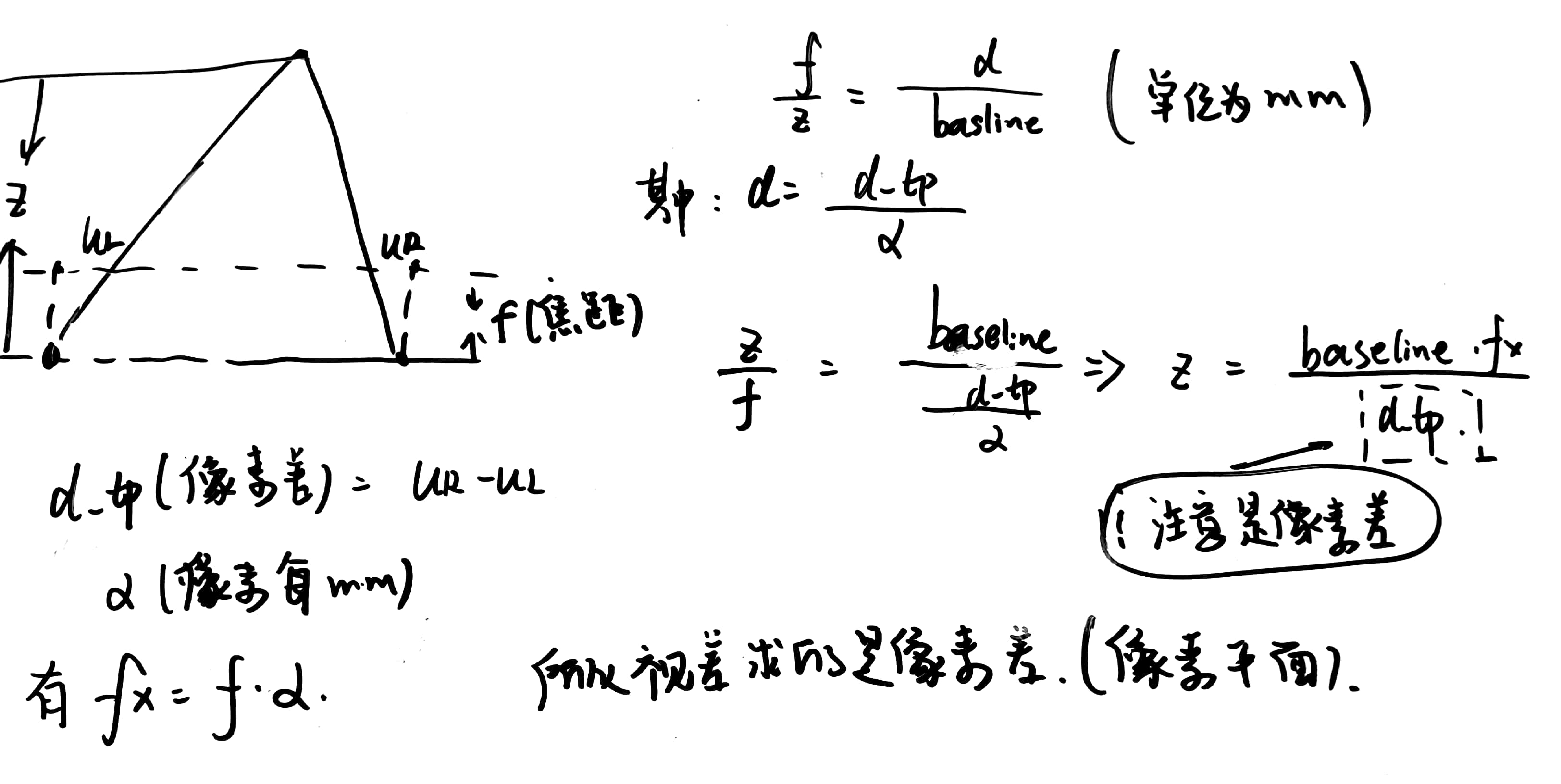
下面介绍立体视觉中的视差与深度之间的关系。
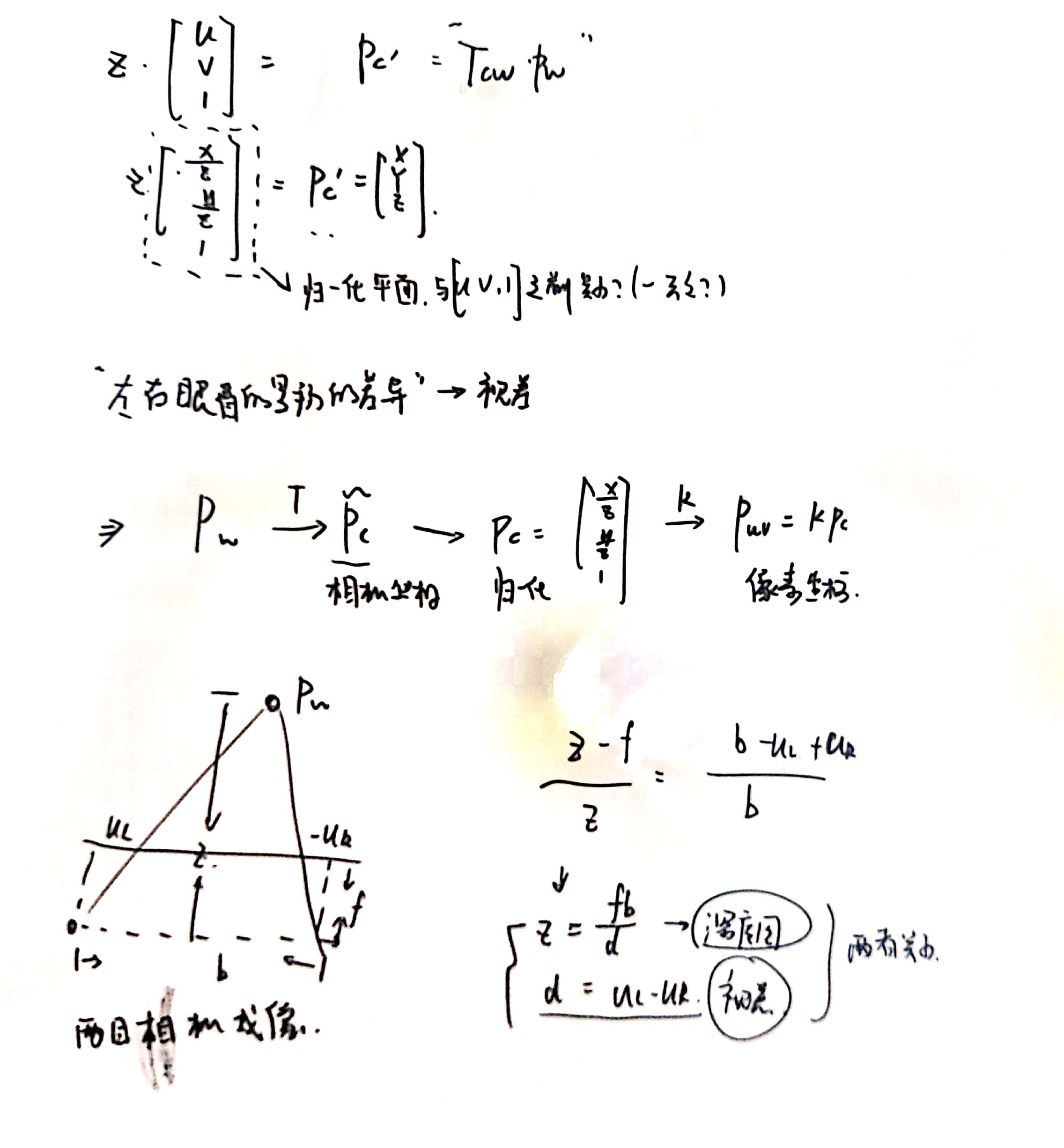
PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道 n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。两张图像中,其中一张特征点的 3D 位置已知,那么最少只需 三个点对(需要至少一个额外点验证结果)就可以估计相机运动。特征点的 3D 位置可以 由三角化,或者由 RGB-D 相机的深度图确定。
因此,在双目或 RGB-D 的视觉里程计中, 我们可以直接使用 PnP 估计相机运动。而在单目视觉里程计中,必须先进行初始化,然后 才能使用 PnP。3D-2D 方法不需要使用对极约束,又可以在很少的匹配点中获得较好的运 动估计,是最重要的一种姿态估计方法。
那么对极几何的几种问题类型如下:

其中比较特别的是:3d-3d。也就是用ICP方法求解。ICP的用法有很多方面,可以去匹配两条轨迹,匹配两个具有深度的图片,以算出“R和T矩阵”。另外,在三维点匹配的时候也很常用。
用图例来表示对极几何问题同样比较直观,下面展示了2d到2d的过程。

双目标定常常用P2P的方法去求解本质矩阵E,来获得双目之间的R和T矩阵。其不会与单目相机一样产生尺度不确定性,因为双目的基线是已知量,可以为其提供尺度。实际上p2p就可以解决两张图片(非深度图)之间的位姿估计,因此常常被用作纯单目的slam中。但是对于相机的运动有所限制,当相机只进行旋转时,那么将无法求解本质矩阵。同时,求解本质矩阵有两种方法–SVD与最小二乘优化SVD(奇异值分解)要求只有8个匹配点,如果矩阵的秩为8,那么可以直接求出解析解。但是最小二乘的方法可以利用更多匹配点信息。针对误匹配的情况,可以用RANSAC方法剔除,,这是一种可以取代最小二乘的通用方法。因此PnP就成为了最重要的方法,他可以利用一张图片的深度信息,活得更准确的位姿估计。
奇异值分解:https://www.cnblogs.com/endlesscoding/p/10033527.html(这个博客写的相当好)
| 求解本质矩阵 的优化算法 |
概述 | 特点 |
|---|---|---|
| SVD | 奇异值分解 | 1. 点数有所限制,必须是八个点 2. 需要满足秩的要求,不然会产生奇异点 |
| 最小二乘 | 最大似然估计/最大后验估计 | 1. 利用算法迭代优化 2. 实际上是曲线拟合,不能剔除错误点 |
| RANSAC | 基于RANSAC的鲁棒方法 | 1. 可以剔除错误点 2. 被广泛采用 |
4. 2D-3D(PnP)与图优化
图优化框架表示如下:

在图优化中均有标准的库可以使用,因此,下面给出书中的实例。
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
// #include <g2o/solvers/csparse/linear_solver_csparse.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
#include <chrono>
using namespace std;
using namespace cv;
void find_feature_matches (
const Mat& img_1, const Mat& img_2,
std::vector<KeyPoint>& keypoints_1,
std::vector<KeyPoint>& keypoints_2,
std::vector< DMatch >& matches );
// 像素坐标转相机归一化坐标
Point2d pixel2cam ( const Point2d& p, const Mat& K );
void bundleAdjustment (
const vector<Point3f> points_3d,
const vector<Point2f> points_2d,
const Mat& K,
Mat& R, Mat& t
);
int main ( int argc, char** argv )
{
if ( argc != 5 )
{
cout<<"usage: pose_estimation_3d2d img1 img2 depth1 depth2"<<endl;
return 1;
}
//-- 读取图像
Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );
vector<KeyPoint> keypoints_1, keypoints_2;
vector<DMatch> matches;
find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
cout<<"一共找到了"<<matches.size() <<"组匹配点"<<endl;
// 建立3D点
Mat d1 = imread ( argv[3], CV_LOAD_IMAGE_UNCHANGED ); // 深度图为16位无符号数,单通道图像
Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
/*内参*/
vector<Point3f> pts_3d;
vector<Point2f> pts_2d;
for ( DMatch m:matches )
{ /*keypoints_1中找到matches到的点,然后就对应上了*/
ushort d = d1.ptr<unsigned short> (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
if ( d == 0 ) // bad depth
continue;
float dd = d/1000.0;
Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );
pts_3d.push_back ( Point3f ( p1.x*dd, p1.y*dd, dd ) );
pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
}
cout<<"3d-2d pairs: "<<pts_3d.size() <<endl;
Mat r, t;
solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false ); // 调用OpenCV 的 PnP 求解,可选择EPNP,DLS等方法
Mat R;
cv::Rodrigues ( r, R ); // r为旋转向量形式,用Rodrigues公式转换为矩阵
cout<<"R="<<endl<<R<<endl;
cout<<"t="<<endl<<t<<endl;
cout<<"calling bundle adjustment"<<endl;
bundleAdjustment ( pts_3d, pts_2d, K, R, t );/*后端?优化的过程?*/
}
void find_feature_matches ( const Mat& img_1, const Mat& img_2,
std::vector<KeyPoint>& keypoints_1,
std::vector<KeyPoint>& keypoints_2,
std::vector< DMatch >& matches )
{
//-- 初始化
Mat descriptors_1, descriptors_2;
// used in OpenCV3
Ptr<FeatureDetector> detector = ORB::create();
Ptr<DescriptorExtractor> descriptor = ORB::create();
// use this if you are in OpenCV2
// Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
// Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create ( "BruteForce-Hamming" );
//-- 第一步:检测 Oriented FAST 角点位置
detector->detect ( img_1,keypoints_1 );
detector->detect ( img_2,keypoints_2 );
//-- 第二步:根据角点位置计算 BRIEF 描述子
descriptor->compute ( img_1, keypoints_1, descriptors_1 );
descriptor->compute ( img_2, keypoints_2, descriptors_2 );
//-- 第三步:对两幅图像中的BRIEF描述子进行匹配,使用 Hamming 距离
vector<DMatch> match;
// BFMatcher matcher ( NORM_HAMMING );
matcher->match ( descriptors_1, descriptors_2, match );
//-- 第四步:匹配点对筛选
double min_dist=10000, max_dist=0;
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for ( int i = 0; i < descriptors_1.rows; i++ )
{
double dist = match[i].distance;
if ( dist < min_dist ) min_dist = dist;
if ( dist > max_dist ) max_dist = dist;
}
printf ( "-- Max dist : %f \n", max_dist );
printf ( "-- Min dist : %f \n", min_dist );
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
for ( int i = 0; i < descriptors_1.rows; i++ )
{
if ( match[i].distance <= max ( 2*min_dist, 30.0 ) )
{
matches.push_back ( match[i] );
}
}
}
Point2d pixel2cam ( const Point2d& p, const Mat& K )
{
return Point2d
(
( p.x - K.at<double> ( 0,2 ) ) / K.at<double> ( 0,0 ),
( p.y - K.at<double> ( 1,2 ) ) / K.at<double> ( 1,1 )
);
}
void bundleAdjustment (
const vector< Point3f > points_3d,
const vector< Point2f > points_2d,
const Mat& K,
Mat& R, Mat& t )
{
// 初始化g2o
typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block; // pose 维度为 6, landmark 维度为 3
/*注意这里的维度设定*/
// Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>(); // 线性方程求解器
Block* solver_ptr = new Block ( linearSolver ); // 矩阵块求解器
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm ( solver );/*初始化完成*/
// vertex
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
Eigen::Matrix3d R_mat;
R_mat <<
R.at<double> ( 0,0 ), R.at<double> ( 0,1 ), R.at<double> ( 0,2 ),
R.at<double> ( 1,0 ), R.at<double> ( 1,1 ), R.at<double> ( 1,2 ),
R.at<double> ( 2,0 ), R.at<double> ( 2,1 ), R.at<double> ( 2,2 );
pose->setId ( 0 );
/*step1: 将相机的位姿输入进去*/
pose->setEstimate ( g2o::SE3Quat (
R_mat,
Eigen::Vector3d ( t.at<double> ( 0,0 ), t.at<double> ( 1,0 ), t.at<double> ( 2,0 ) )
) );
optimizer.addVertex ( pose );
int index = 1;
/*points_3d step2:将路标点输入进去*/
//注意这里有很多歌路标点的
for ( const Point3f p:points_3d ) // landmarks
{
g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
point->setId ( index++ );
point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容,(信息矩阵)
optimizer.addVertex ( point );
}
// parameter: camera intrinsics
g2o::CameraParameters* camera = new g2o::CameraParameters (
K.at<double> ( 0,0 ), Eigen::Vector2d ( K.at<double> ( 0,2 ), K.at<double> ( 1,2 ) ), 0
);
camera->setId ( 0 );
optimizer.addParameter ( camera );
// edges
index = 1;
for ( const Point2f p:points_2d )
{
g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
edge->setId ( index );
edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
edge->setVertex ( 1, pose );
edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
edge->setParameterId ( 0,0 );
edge->setInformation ( Eigen::Matrix2d::Identity() );
optimizer.addEdge ( edge );
index++;
}
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.setVerbose ( true );
optimizer.initializeOptimization();
optimizer.optimize ( 100 );
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> ( t2-t1 );
cout<<"optimization costs time: "<<time_used.count() <<" seconds."<<endl;
cout<<endl<<"after optimization:"<<endl;
cout<<"T="<<endl<<Eigen::Isometry3d ( pose->estimate() ).matrix() <<endl;
//Eigen::Isometry3d ( pose->estimate() ).matrix() 就可以得到最终的矩阵
}
cmake文件如下:
cmake_minimum_required( VERSION 2.8 )
project( vo1 )
set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )
# 添加cmake模块以使用g2o
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )
find_package( OpenCV 3.1 REQUIRED )
# find_package( OpenCV REQUIRED ) # use this if in OpenCV2
find_package( G2O REQUIRED )
#find_package( CSparse REQUIRED )
include_directories(
${OpenCV_INCLUDE_DIRS}
${G2O_INCLUDE_DIRS}
# ${CSPARSE_INCLUDE_DIR}
"/usr/include/eigen3/"
)
add_executable( pose_estimation_3d2d pose_estimation_3d2d.cpp )
target_link_libraries( pose_estimation_3d2d
${OpenCV_LIBS}
${CSPARSE_LIBRARY}
g2o_core g2o_stuff g2o_types_sba g2o_csparse_extension
)
5. aruco图片处理
std::vector<std::vector<cv::Point2f>> marker_corners;
std::vector<int> IDs;
std::vector<cv::Vec3d> rvs, tvs;
cv::aruco::detectMarkers(img, dictionary_ , marker_corners, IDs);
cv::aruco::estimatePoseSingleMarkers(marker_corners, marker_length_, K_, dist_, rvs, tvs);
cv::Rodrigues(rvec, R);
///得到tcm
Eigen::Matrix4d T_c_m;





